Inspiration

Much like Wordle, Spelling Bee, and the crossword, I had often played NYT’s Letter Boxed game. I had often thought of building my own Norwegian version of it, but it wasn’t immediately obvious how such a system would work.

I let it percolate in my brain for a while until I sat down and just started writing code to see what it would take. There were a lot of false-starts, but I eventually wound up somewhere that I was happy with.

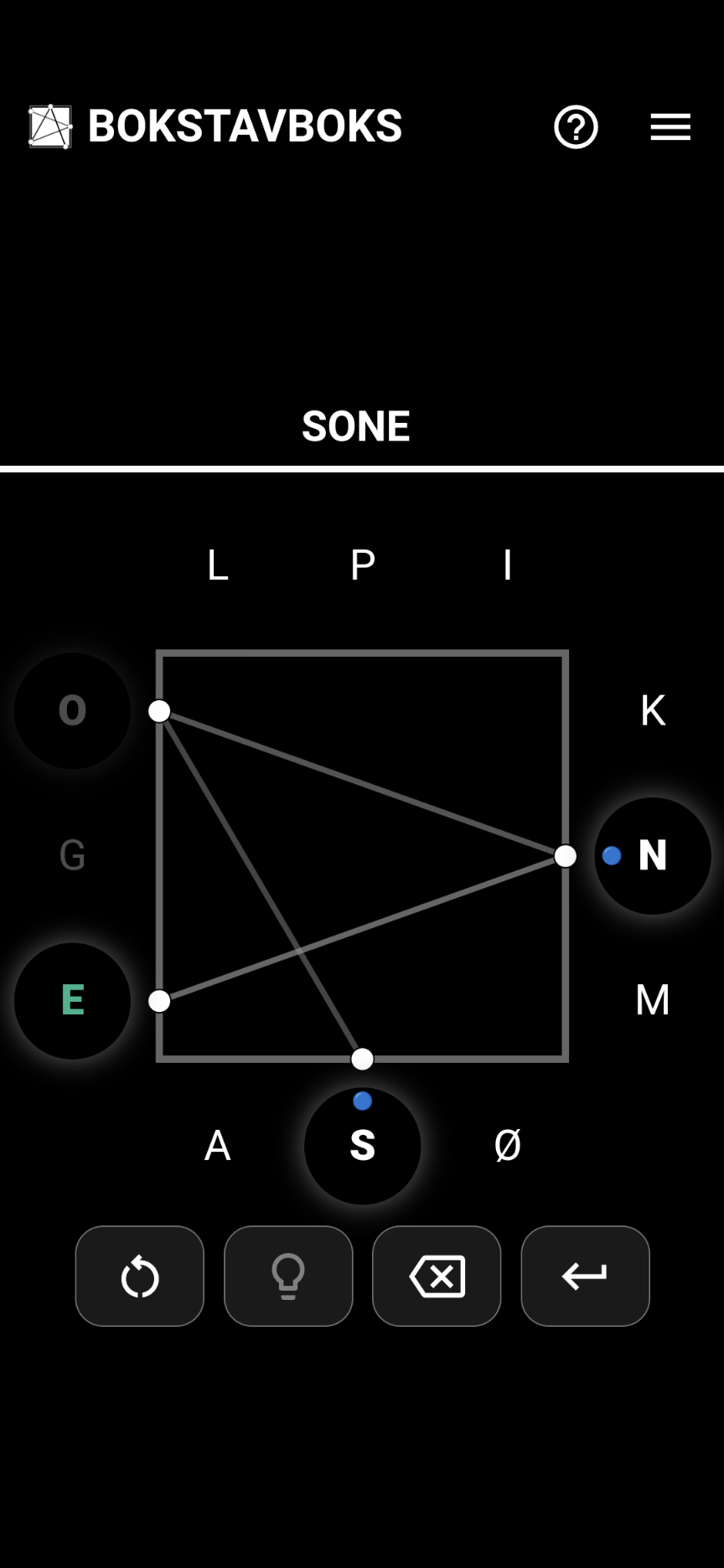
A modern playable version

A modern playable version

Process

At a high level, the way the app works on page load is:

  1. Construct a board
  2. Solve the board
  3. Present the board to the user for them to play

This rather circuitous approach is necessary because there are no guarantees that:

  • a random board of 12 letters can be solved; or
  • a board constructed from two words cannot be solved with one word

As a result, it was necessary to do the extra steps.

Generating a board

To generate a board, the general flow is outlined below. For the purposes of this text, I’m going to represent a given square like this:

_ _ _ | _ _ _ | _ _ _ | _ _ _
 top  | right |bottom | left

Each block of three _ characters is a side of the square, in clockwise order. Initially, there are no letters, so each side is empty.

  1. Pick a random1 word: ABCDEF...

  2. Take A and place it on the top side of the square

    A _ _ | _ _ _ | _ _ _ | _ _ _

  3. Take B and place it on the right side of the square

    A _ _ | B _ _ | _ _ _ | _ _ _

  4. Take C and:

    1. Create three parallel universes

    2. In the first one, place it on the top side

      A C _ | B _ _ | _ _ _ | _ _ _

    3. In the second one, place it on the bottom side

      A _ _ | B _ _ | C _ _ | _ _ _

    4. In the fourth one, place it on the left side

      A _ _ | B _ _ | _ _ _ | C _ _

    In short, we’re putting C in all possible positions.

  5. Take D and:

    1. For each of our parallel universes, create three more universes

    2. Add D into all possible positions

      A C _ | B D _ | _ _ _ | _ _ _
A C _ | B _ _ | D _ _ | _ _ _
A C _ | B _ _ | _ _ _ | D _ _
A D _ | B _ _ | C _ _ | _ _ _
A _ _ | B D _ | C _ _ | _ _ _
A _ _ | B _ _ | C _ _ | D _ _
A D _ | B _ _ | _ _ _ | C _ _
A _ _ | B D _ | _ _ _ | C _ _
A _ _ | B _ _ | D _ _ | C _ _

  6. Continue like this for the rest of the letters in the word

  7. If all 12 positions are filled, then we have constructed a puzzle with a known solution (even if suboptimal)

  8. If we ran out of letters in the word, pick another word at random1 – but one which starts with the ending letter of the previous word.

  9. GOTO 1

In theory, this could take a very long time. It’s probably possible to construct pathological inputs to make this take an infinite amount of time – any time you’re looping over randomly-chosen data, it’s a bit suspicious.

However, I built in an escape-hatch: if it’s ever exceeding a certain number of loops, just throw the whole thing away and start fresh. This isn’t perfect, but it’s at least a way to hopefully avoid thrashing the user’s computer.

(Remember: all of this happens in the user’s browser)

Solving a puzzle

Finding the optimal solution to the puzzle is the next challenge. The puzzle was generated from many randomly-chosen words, but it’s probable that there exists a more-optimal solution to the puzzle.

At a high level, the process looks like this:

  1. Filter the dictionary to words which are playable on a given puzzle
    • Words which consist of letters on the square
    • Words which do not have consecutive letters on the same side of the square
  2. Sort the playable words from “best” to “worst”
    • If a word has more of the 12 letters than another word, it is better than another word which has fewer.
    • If a word has equal numbers of the 12 letters than another word, the shorter word is better than another word which is longer.
  3. Play all of the words on their own boards
  4. If any boards are solved, you have found a solution
    • The shortest word is the best solution
  5. For each board, re-sort the words from “best” to “worst”:
    • If a word has more of the remaining letters than another word, it is better than another word which has fewer
    • If a word is shorter than other word, then it is better than a longer word.
  6. For each board, create new boards for all of their second-word options
  7. GOTO 4

Just like with the generation process, this has the possibility to end badly. For example, if a board took N words to construct2, the combinatorial explosion of boards being solved in parallel would be terrible for performance.

The escape-hatch for this step is different: I gave the user a “cancel” button and they can just generate a new board.

I’m not happy about this and I am sure that there exists a more efficient solving method, but fixing it hasn’t become a priority for me. In my testing, I see more than 3 word solutions extremely rarely.

Building the app

With those breakthroughs out of the way, all that was left was the app. This was relatively straightforward, though I did learn quite a bit about workers and background processing on the web along the way.

Reflections

This project was exceedingly fun for me. I really enjoyed the process of discovery for generating the board, solving the board, and then showing it to the user. This was an entirely different beast than [Ordle] and [Stavehumle] which were much simpler.

I also really enjoy the style of gameplay: there is no longer a single “correct” answer which you must find. Instead, players can find many valid solutions, and strive to find better ones. If a player has a limited vocabulary (🙋), they won’t be unable to solve it – they just might have a different solution than someone else.

  1. Not actually random. Instead, I’m using a pseudo-random number generator that has ben seeded with a puzzle-specific seed so all players with that seed will get the same output. ↩︎ ↩︎

  2. There’s a minimum word length of 2, so N is at most six ↩︎